Matematyka - od podstaw do matury

ELEMENTY KOMBINATORYKI

W tym podrozdziale przedstawimy metody obliczania mocy zbiorów przestrzeni zdarzeń elementarnych i zdarzenia losowego, stosowane w sytuacjach, gdy są to wielkości tak duże, że wypisanie wszystkich zdarzeń elementarnych zajęło by ogromnie dużo miejsca i czasu.
Na poziomie podstawowym obowiązuje nas znajomość czterech podstawowych „narzędzi” kombinatoryki:
- zasada mnożenia,
- permutacje,
- wariacja z powtórzeniami,
- wariacja bez powtórzeń.

Przedstawimy kolejno każde z nich:

ZASADA MNOŻENIA

Stosujemy ją, gdy zdarzenie jest ciągiem kilku elementów (liczb, liter itp.), a każdy element losujemy z konkretnego zbioru.
Liczbę elementów konkretnego zbioru oznaczamy literą k.

Przykład:
Dla każdego psa na wystawie losowany jest numer identyfikacyjny, składający się z liczby z zakresu od jeden do dziewięciu oraz litery alfabetu ze zbioru: A, B, C, D, E, F, G, H, I, J, K.
Zdarzenie elementarne składa się więc z ciągu: [cyfra, litera], które losujemy z podanych zbiorów.
Liczba elementów w ciągu wynosi 2.
Liczba elementów pierwszego zbioru, zawierającego cyfry od 1 do 9, wynosi 9 (jest 9 cyfr):

Liczba elementów drugiego zbioru, zawierającego podane litery, wynosi 11 (jest 11 liter).


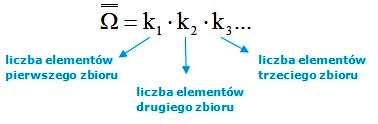
Liczba wszystkich zdarzeń ( ) jest iloczynem liczb elementów wszystkich zbiorów.

Liczba wszystkich zdarzeń z przykładu będzie wynosić:


Obliczymy prawdopodobieństwo zdarzenia losowego A, polegającego na wylosowaniu numeru identyfikacyjnego, którego cyfra jest nieparzysta.

PERMUTACJE

Mamy z nimi do czynienia, gdy określamy liczbę wszystkich ciągów, jakie możemy utworzyć z wszystkich elementów danego zbioru. Kluczowa jest liczba elementów tego zbioru, którą oznaczamy literą n
Jedno zdarzenie elementarne jest jednym konkretnym ciągiem, jaki możemy otrzymać.

Przykład:
Losowo umieszczamy 8 różnokolorowych (niebieskie, białe, czarne, czerwone, zielone, żółte, fioletowe i pomarańczowe) pudełek w szeregu. Określimy ile istnieje możliwości ustawienia pudełek.
Liczba elementów zbioru, z którego tworzymy ciąg wynosi 8:
n = 8

Liczbę wszystkich możliwych zdarzeń elementarnych (liczbę permutacji) obliczamy ze wzoru:



Silnia jest działaniem, którego wynikiem jest iloczyn liczb całkowitych od liczby 1 do danej liczby:



Dla rozpatrywanego przykładu:


Zdarzenie losowe także może być obliczane za pomocą wzoru permutacji.
Przykład:
Obliczymy prawdopodobieństwo zdarzenia losowego polegającego na uzyskaniu szeregu, w którym drugim pudełkiem jest pudełko zielone.

WARIACJE BEZ POWTÓRZEŃ

Z wariacją bez powtórzeń mamy do czynienia, gdy tworzymy ciąg z elementów danego zbioru, ale ciąg nie musi składać się ze wszystkich elementów zbioru. Przykładowo w zbiorze może znajdować się dziesięć elementów, a powstały ciąg jest trzyelementowy.
Zwrot „bez powtórzeń” oznacza, że żaden element w powstałym ciągu nie może się powtarzać. W przypadku losowania kolejnych elementów ciągu, element już wylosowany nie wraca do puli i nie może zostać wylosowany ponownie (jest to tzw. losowanie bez zwracania).

W przypadku, gdy ciąg będzie składał się z wszystkich elementów zbioru, dana wariacja będzie jednocześnie permutacją (opisaną powyżej).
Liczbę elementów zbioru oznaczamy literą n.
Liczbę elementów wariacji (powstałego ciągu) oznaczamy literą k.

Przykład:
Każdemu pracownikowi przydzielony jest trzycyfrowy kod identyfikacyjny złożony z cyfr od 1 do 9, przy czym żadna cyfra w kodzie nie może się powtarzać.
Liczba elementów zbioru, z którego losujemy elementy ciągu wynosi 9 (mamy 9 cyfr):

Liczba elementów ciągu wynosi 3 (kod zawiera 3 cyfry).


Wariację bez powtórzeń oznaczamy symbolem:

Liczbę wszystkich możliwych wariacji bez powtórzeń obliczamy ze wzoru: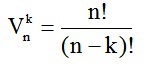


Dla rozpatrywanego przykładu:



UWAGA: Mając do wykonania powyższe działanie, nie obliczajmy od razu silni z liczb w liczniku i mianowniku. Najpierw powinniśmy uprościć dane wyrażenie (może się to okazać niezbędne – dla zbyt dużych liczb wynik działania „silni” nie zmieści się na ekranie kalkulatora).
W tym celu silnię większej liczby (9!) rozkładamy na silnię mniejszej liczby (6!) oraz iloczyn odpowiednich liczb:


Obliczymy prawdopodobieństwo zdarzenia losowego, polegającego na uzyskaniu kodu, w którym pierwsza cyfra, to cyfra 6

WARIACJE Z POWTÓRZENIAMI

Z wariacją z powtórzeniami mamy do czynienia, gdy tworzymy ciąg z elementów danego zbioru, ale ciąg nie musi składać się ze wszystkich elementów zbioru, czyli tak jak w przypadku wariacji bez powtórzeń.
Różnica polega na tym, że elementy w powstałym ciągu mogą się powtarzać. W momencie losowania kolejnych elementów ciągu, element wylosowany wraca do puli i może zostać wylosowany ponownie (jest to tzw. losowanie ze zwracaniem)

Liczbę elementów zbioru oznaczamy literą n.
Liczbę elementów wariacji (powstałego ciągu) oznaczamy literą k.

Przykład:
Kod alarmu składa się z 4 cyfr, z zakresu cyfr od 1 do 9.
Jest to przykład wariacji z powtórzeniami, ponieważ tworzymy ciąg czteroelementowy z dziewięciu cyfr, przy czym każda cyfra może się powtarzać.

Liczba elementów zbioru, z którego losujemy elementy ciągu wynosi 9 (mamy 9 cyfr):

Liczba elementów ciągu wynosi 4 (kod zawiera 4 cyfry).


Wariację z powtórzeniami oznaczamy symbolem:

Liczbę wszystkich możliwych wariacji z powtórzeniami obliczamy ze wzoru:


Dla rozpatrywanego przykładu:


Obliczymy prawdopodobieństwo zdarzenia losowego, polegającego na uzyskaniu kodu, w którym pierwsza cyfra wynosi 3 lub 5.

WYBÓR PODEJŚCIA

Poniżej zestawiamy warunki zastosowania poszczególnych podejść wraz ze wzorami:

Zasada mnożenia
Zdarzenie elementarne to ciąg elementów, z których każdy losowany jest z innego zbioru o określonej liczbie elementów

Liczbę zdarzeń elementarnych obliczamy ze wzoru, w którym k1, k2, k3… to liczba elementów poszczególnych zbiorów:

Wariacje bez powtórzeń
Zdarzenie elementarne to ciąg elementów, powstały poprzez wylosowanie kilku elementów z danego zbioru, przy czym żaden element w powstałym ciągu nie może się powtarzać.

Liczbę zdarzeń elementarnych, obliczamy ze wzoru, w którym n to liczba elementów zbioru z którego losujemy, a k to liczba elementów powstałego ciągu: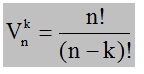

Permutacje
Zdarzenie elementarne to ciąg elementów, powstały poprzez uszeregowanie wszystkich elementów danego zbioru.

Liczbę zdarzeń elementarnych, obliczamy ze wzoru, w którym n to liczba elementów zbioru:

Wariacje z powtórzeniami
Zdarzenie elementarne to ciąg elementów, powstały poprzez wylosowanie kilku elementów z danego zbioru, przy czym elementy w powstałym ciągu mogą się powtarzać.

Liczbę zdarzeń elementarnych obliczamy ze wzoru, w którym n to liczba elementów zbioru z którego losujemy, a k to liczba elementów powstałego ciągu:

Nie jest tak, że konkretne zadanie można rozwiązać za pomocą wyłącznie jednego podejścia. Zasada mnożenia ma zastosowanie we wszystkich typach zadań, z jakimi mamy do czynienia w zakresie matury podstawowej!
Zasada mnożenia okazuje się dość wygodna do obliczania mocy zbioru zdarzenia losowego.
Możemy spotkać się z zadaniami, w których moc przestrzeni zdarzeń elementarnych będzie kwalifikować się do obliczenia jednym ze wzorów na wariację, a moc zdarzenia losowego będzie najłatwiejsza do obliczenia za pomocą zasady mnożenia.