Matematyka - od podstaw do matury

WARUNEK PROSTOPADŁOŚCI PROSTYCH
Matematyka – matura - geometria analityczna (funkcja liniowa): równanie prostej, warunek prostopadłości prostych

Warunek prostopadłości, ma także dwie wersje: dla postaci kierunkowej i ogólnej i tu także zalecanym przez nas podejściem, jest korzystanie z warunku dla postaci kierunkowej.


Postać kierunkowa
Dwie proste są prostopadłe, gdy ich współczynniki kierunkowe mają przeciwne znaki i są w stosunku do siebie liczbami odwrotnymi.
Brzmi to skomplikowanie, ale w praktyce jest całkiem proste.

Przykładowo: jeżeli współczynnik kierunkowy pierwszej funkcji wynosi 4, to współczynnik kierunkowej drugiej powinien wynosić:


Przykład:


Proste k oraz l są prostopadłe ( l k).

Postać ogólna
Dwie proste są prostopadłe, gdy ich współczynniki liczbowe spełniają równość: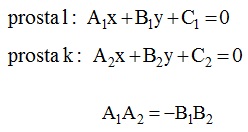

Przykład:


Warunek prostopadłości tak jak warunek równoległości, wykorzystuje się jeszcze w dwóch sytuacjach:
- w celu określenia wzoru funkcji prostej prostopadłej do danej, co przedstawimy w tym punkcie,
- w zadaniach z parametrem (co zostanie przedstawione w podrozdziale: zadania z parametrem).

Obliczanie wzoru prostej prostopadłej do danej.
Mowa tu o zadaniach, w których podana jest funkcja, do której szukana prosta jest prostopadła oraz punkt przez jaki przechodzi.
Przykład:
Podaj wzór prostej prostopadłej do prostej: y = 3x -5, jeżeli przechodzi ona przez punkt (-6, 5).

Dla tego zadania, osobno przedstawimy dwa podejścia – z pozycji postaci kierunkowej i ogólnej.

Postać kierunkowa
Aby poznać wzór prostej zapisanej pod postacią kierunkowej, musimy obliczyć jej współczynniki (a i b).
Na wstępie nie znamy wartości żadnego z nich. Możemy jedynie zapisać kierunkowy wzór funkcji liniowej:


Korzystamy z informacji zawartych w zadaniu.
Po pierwsze: prosta ma być prostopadła do prostej y = 3x -5. Oznacza to, że współczynnik kierunkowy szukanej funkcji powinien być liczbą przeciwną i odwrotną do liczby 3, czyli: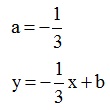

W tym momencie brakuje nam jeszcze wartości współczynnika „b”

Po drugie: szukana prosta, przechodzi przez punkt (-6, 5). Możemy podstawić współrzędne punktu do wzoru i z tak powstałego równania obliczyć „b”.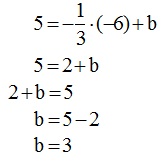

Gdy znamy współczynnik „b”, wystarczy podstawić go do wzoru i w ten sposób otrzymujemy pełny wzór szukanej prostej:

Postać ogólna
Musimy najpierw przekształcić wzór funkcji do postaci ogólnej:

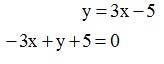
Tu także, aby móc zapisać wzór prostej, musimy określić jej współczynniki (A, B i C).


Korzystamy z informacji zawartych w zadaniu.
Po pierwsze: prosta ma być prostopadła do prostej -3x + y + 5 = 0.

Korzystamy z zależności:
- współczynnik B szukanej funkcji jest równy współczynnikowi A podanej funkcji:
B = -3
- współczynnik A szukanej funkcji jest równy współczynnikowi B danej funkcji o przeciwnym znaku:
A = -1



W tym momencie brakuje nam jeszcze wartości współczynnika „C”

Po drugie: szukana prosta, przechodzi przez punkt (-6, 5). Możemy podstawić współrzędne punktu do wzoru i z tak powstałego równania obliczyć „C”.

Gdy znamy współczynnik „C”, wystarczy podstawić go do wzoru i w ten sposób otrzymujemy pełny wzór szukanej prostej:

W przypadku jakichkolwiek pytań zapraszamy na nasze forum :)