Matematyka - od podstaw do matury

DZIAŁANIA NA WIELOMIANACH
Matematyka – matura - wielomiany: działania na wielomianach (dodawanie, odejmowanie, mnożenie)

Działania na wielomianach nie różnią się w zasadzie niczym od działań, jakie wykonujemy na innych wyrażeniach algebraicznych. Omówimy trzy podstawowe działania (dodawanie, odejmowanie, mnożenie). Dzielenie wielomianów jest bardziej skomplikowane i nie wchodzi w zakres matury podstawowej.

Wszystkie trzy działania przedstawimy na przykładzie dwóch wielomianów:

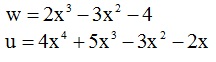
Dodawanie wielomianów
Dodajemy wielomiany zgodnie z zasadami działań na wyrażeniach algebraicznych (dodajemy wyrażenia podobne - rozdział w dziale "podstawy": wyrażenia algebraiczne). Otrzymane wyrażenia szeregujemy w kolejności od największej do najmniejszej potęgi.



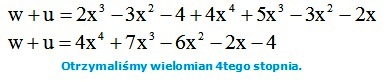
***Stopień otrzymanego wielomianu jest zazwyczaj równy stopniu wielomianu o wyższym stopniu. Tak jest w rozpatrywanym przykładzie: st(w) = 3, st(u) = 4, a stopień ich sumy jest równy stopniu „wyższego” wielomianu: st(w + u) = 4.Ta zasada jest zawsze prawdziwa, gdy dodajemy wielomiany o różnych stopniach.
Gdy dodawane wielomiany mają ten sam stopień, może się zdarzyć, że najwyższe potęgi wielomianów się nawzajem zredukują! W takim wypadku, aby określić stopień sumy wielomianów należy wykonać dodawanie.

Odejmowanie wielomianów
Właśnie w przypadku odejmowania wielomianów pojawia się najwięcej błędów. Należy pamiętać, aby zawsze odejmując od siebie dwa wielomiany, drugi zapisać w nawiasie (minus przed nawiasem w następnym kroku zmieni nam wszystkie znaki).

***Stopień otrzymanego wielomianu zależy od wielomianów składowych, w taki sam sposób jak wypadku dodawania.

Mnożenie wielomianów
W celu przemnożenia przez siebie dwóch wielomianów, oba musimy zapisać w nawiasie. Mnożenie wykonujemy zgodnie z zasadami działań na wyrażeniach algebraicznych, czyli mnożymy każde wyrażenie przez każde.

***Stopień otrzymanego wielomianu jest równy sumie stopni składowych wielomianów.
Wielomiany z przykładu mają stopnie: st(w) = 3, st(u) = 4. Stopień iloczynu tych wielomianów można określić dodając stopnie obu wielomianów: 3 + 4 = 7.

Złożone działania
Oczywiście na wielomianach możemy wykonywać bardziej złożone działania. Należy kierować się wyżej przedstawionymi zasadami oraz kolejnością wykonywania działań.
Przykład:
Dla wielomianów: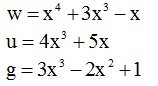

Wykonaj działanie: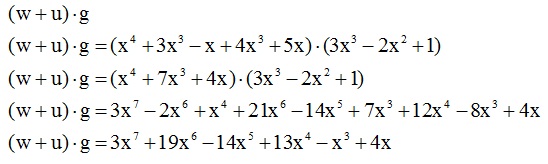


***Stopień otrzymanego wielomianu, możemy określić zgodnie z wcześniej przedstawionymi zasadami. Dodając wielomiany w (4 stopień) oraz u (3 stopień), otrzymamy wielomian 4 stopnia. Mnożąc ten wielomian przez wielomian g (3 stopień) musimy więc otrzymać wielomian 7 stopnia.

W przypadku jakichkolwiek pytań zapraszamy na nasze forum :)