Matematyka - od podstaw do matury
Menu główne:
- O STRONIE
- PODSTAWY
- MATERIAŁ MATURALNY
- potęgi i pierwiastki
- wyrażenia algebraiczne
- procenty
- zbiory i przedziały
- wartość bezwzględna
- przybliżenia
- funkcje
- f. liniowa, geometria analityczna
- funkcja kwadratowa
- wielomiany
- funkcja wykładnicza
- logarytmy
- wyrażenia wymierne
- funkcja wymierna
- ciągi
- funkcje trygonometryczne
- planimetria (figury płaskie)
- stereometria (bryły)
- prawdopodobieństwo
- statystyka
- KOMPENDIUM
- KONTAKT
- FORUM
dziedzina wyrażeń wymiernych - matematyka, matura
MATERIAŁ MATURALNY > wyrażenia wymierne
DZIEDZINA WYRAŻENIA WYMIERNEGO
Matematyka – matura - wyrażenia wymierne: dziedzina wyrażenia wymiernego
Wyrażenie wymierne to iloraz dwóch wielomianów. Jest więc wyrażeniem ułamkowym, w którym w mianowniku lub liczniku znajdują się wyrażenia z „x”.
Przykłady: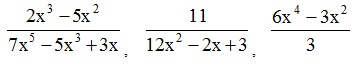
Zanim wykonamy jakiekolwiek działanie na wyrażeniach wymiernych, musimy określić dziedzinę wyrażeń! (Przypominamy: w mianowniku nie może znajdować się zero, dlatego z dziedziny, wykluczamy miejsca zerowe mianownika).
Sprowadza się to do obliczenia równania: mianownik ![]() 0. Rozwiązaniem równania są liczby, jakie wykluczamy z dziedziny.
0. Rozwiązaniem równania są liczby, jakie wykluczamy z dziedziny.
Równanie jakie będziemy musieli obliczyć, może być równaniem liniowym, kwadratowym, a nawet wielomianowym (z tymi ostatnimi raczej się nie spotkamy). Sposób rozwiązania równania zależy od jego rodzaju, co omówiliśmy w poprzednich rozdziałach ( równania, równania kwadratowe, równania wielomianowe).
Określanie dziedziny wyrażenia wymiernego przedstawimy na przykładach:
Przykład 1.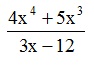
1) Zapisujemy i rozwiązujemy równanie.

2) Zapisujemy dziedzinę, którą będzie zbiór liczb rzeczywistych (R), z wyłączeniem zbioru zawierającego obliczoną z równania wartość (lub wartości, jeżeli rozwiązań równania jest więcej niż jedno).
Przykład 2

UWAGA: Gdy w mianowniku wyrażenia wymiernego znajduje się tylko liczba, nie zapisujemy równania (i tak nie będzie miało rozwiązań). Dziedzina nie ulega więc żadnemu ograniczeniu i jest zbiorem liczb rzeczywistych.
Przykład: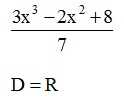
Dziedzina złożonych działań
W następnych podrozdziałach będziemy wykonywać działania na wyrażeniach wymiernych (dodawanie, odejmowanie, mnożenie…). Będziemy musieli wtedy wyznaczyć dziedzinę dla całego działania, a więc wspólną dziedzinę dla wszystkich wyrażeń zawartych w działaniu.
UWAGA: W trakcie obliczeń będziemy zamieniać dzielenie na mnożenie i obracać drugie wyrażenie, dlatego licznik znajdzie się w mianowniku. Gdy mamy do czynienia z dzieleniem, nie tylko mianowniki wyrażeń mają być różne od zera, ale także liczniki dzielnika (wyrażenie przez które dzielimy i które będziemy obracać)!
Przykład:
Mając do wykonania działanie: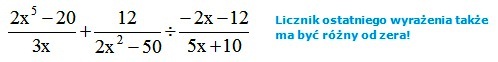
- najpierw wyznaczamy wspólną dziedzinę, dla wszystkich trzech wyrażeń.
Polega to na obliczeniu kliku (tutaj trzech) równań. Dziedzina całego działania, będzie zbiorem liczb rzeczywistych minus zbiór wszystkich liczb, jakie otrzymamy po rozwiązaniu równań.
W przypadku jakichkolwiek pytań zapraszamy na nasze forum :)
Podmenu:
- dziedzina wyrażenia ←
- upraszczanie wyrażeń
- działania na wyrażeniach
- równania wymierne
- ZADANIA