Matematyka - od podstaw do matury
Menu główne:
- O STRONIE
- PODSTAWY
- MATERIAŁ MATURALNY
- potęgi i pierwiastki
- wyrażenia algebraiczne
- procenty
- zbiory i przedziały
- wartość bezwzględna
- przybliżenia
- funkcje
- f. liniowa, geometria analityczna
- funkcja kwadratowa
- wielomiany
- funkcja wykładnicza
- logarytmy
- wyrażenia wymierne
- funkcja wymierna
- ciągi
- funkcje trygonometryczne
- planimetria (figury płaskie)
- stereometria (bryły)
- prawdopodobieństwo
- statystyka
- KOMPENDIUM
- KONTAKT
- FORUM
ciągi - podstawy - matematyka, matura
MATERIAŁ MATURALNY > ciągi
PODSTAWOWE INFORMACJE
Ciąg jest specyficznym rodzajem funkcji.
Argumenty ciągu oznaczamy symbolem n – są to liczby naturalne, dodatnie
( 1, 2, 3 . . .)
Wartości będziemy nazywać wyrazami ciągu – oznaczamy je symbolem an.
Konkretny ciąg, jak każda funkcja może być opisany wzorem.
Przykład:

Podstawiając za „n” kolejne liczby naturalne, otrzymujemy kolejne wyrazy ciągu.
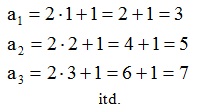
Przykładowo, gdy w zadaniu mamy podać ósmy wyraz ciągu, obliczamy jego wartość dla
n = 8.![]()
Ciąg może również być zapisany jako szereg wyrażeń po przecinku. Wyrażenia te są wówczas kolejnymi wyrazami ciągu.
Przykład:
Dany jest ciąg:
3, 6, 9, 12, 15 . . .
Z podanego w ten sposób ciągu możemy wypisać jego poszczególne wyrazy (tu: pięć pierwszych wyrazów), a nawet ustalić wzór ciągu, który jest konieczny do obliczania innych wyrazów ciągu.![]()
Określenie wzoru ciągu wymaga trochę matematycznej wyobraźni.
Przede wszystkim należy zauważyć, że wartość każdego wyrazu jest równa jego numerowi przemnożonemu przez trzy (czyli n razy 3). Możemy zapisać więc wzór ciągu:![]()
Mając dany wzór możemy obliczyć wartość dowolnego wyrazu ciągu. Przykładowo, obliczymy dwudziesty wyraz ciągu:![]()
Do opisu ciągu można również zastosować sposób słowny, choć rzadko będziemy się z nim spotykać.
Przykład:
Każdej liczbie naturalnej przyporządkuj liczbę o 4 większą.
Na podstawie opisu słownego należy przede wszystkim określić wzór ciągu. Jest to zdecydowanie prostsze niż w przypadku szeregu liczb, gdzie sami musimy ustalić jakie działania miały miejsce.
Tu mamy to wprost podane („przyporządkuj liczbę o 4 większą”). Ciąg będzie miał wzór:
![]()