Matematyka - od podstaw do matury

KĄTY
Zagadnienia: matematyka - podstawówka, gimnazjum - figury płaskie, kąty

Kąt składa się z ramion i wierzchołka. Jego wielkość jest mierzona w stopniach:

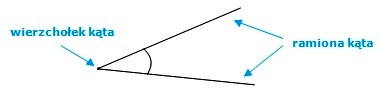
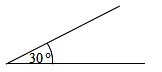
Kąt możemy opisać wpisując w łuk jego miarę (gdy jest znana).
Przykład:

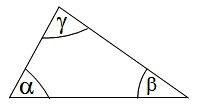
Gdy nie znamy miary kąta, oznaczamy go jedną z greckich liter np: (alfa), (beta),
(gamma) , (delta) .
Przykład:

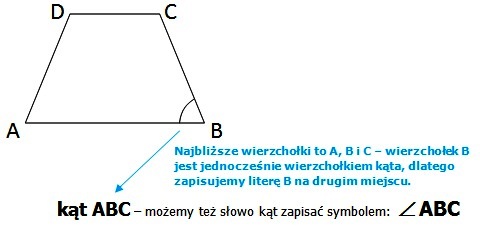
W przypadku kątów zawartych w figurach płaskich, mamy jeszcze jedną możliwość – opisanie kąta dużymi literami, pochodzącymi od wierzchołków figury.
Musimy w pierwszej kolejności opisać figurę dużymi literami, a następnie tworzymy nazwę kątów, która składa się z trzech liter najbliższych wierzchołków, przy czym literę stojącą przy wierzchołku kąta, stawiamy w nazwie kąta na drugim miejscu.
Przykład:

Podział kątów
Kąty dzielimy na podstawie ich miary: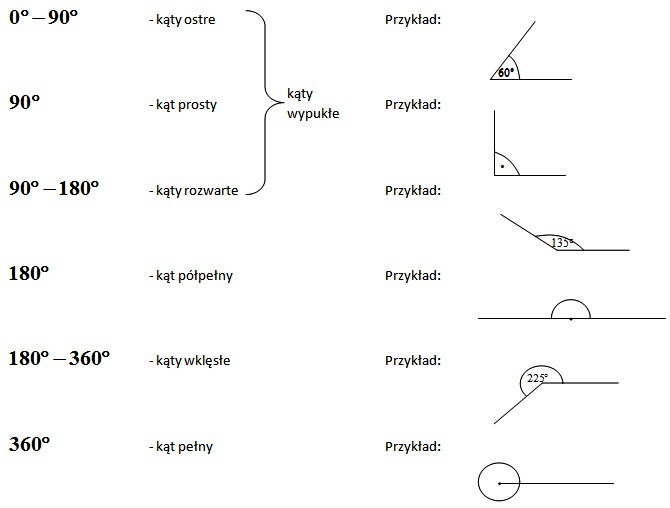

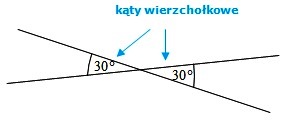
Kąty wierzchołkowe
Kąty wierzchołkowe - to kąty powstałe poprzez przecięcie się dwóch prostych. Kąty wierzchołkowe mają taką samą miarę.
Przykład:

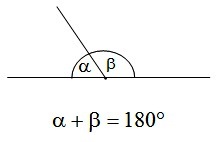
Kąty przyległe
Kąty przyległe - to kąty „leżące” na jednej prostej. Ich suma wynosi

Przykład:
Oblicz miarę kąta , jeżeli kąt ma oraz wiedząc, że są to kąty przyległe.

dane:


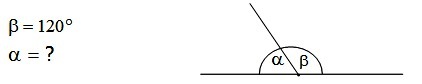
obliczenia:

Kąty naprzemianległe i odpowiadające
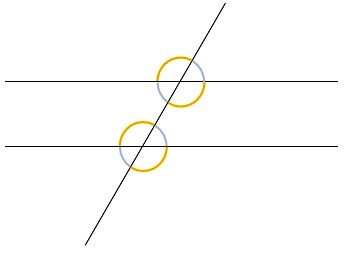
Z kątami naprzemianległymi mamy do czynienia, gdy dwie proste równoległe zostaną przecięte trzecią prostą.

Kąty odpowiadające – to dwa kąty leżące w „ tym samym” miejscu, ale na innej prostej.

Kąty naprzemianległe – kąt
jest naprzemianległy w stosunku do danego, gdy jest kątem wierzchołkowym do kąta odpowiadającego.

Kąty odpowiadające i naprzemianległe mają taką samą miarę. W związku z tym w układzie dwóch prostych równoległych przeciętych trzecią prostą, mamy do czynienia z dwoma miarami kątów – kątów tej samej miary są dwie pary. Te same kąty przedstawimy na rysunku (są oznaczone tym samym kolorem):

W przypadku jakichkolwiek pytań zapraszamy na nasze forum :)